Quantitative analysts constantly seek robust methods to model and predict asset price movements. One such powerful tool is Itô’s Lemma, a cornerstone of stochastic calculus. By leveraging this mathematical framework alongside Python, quants can enhance their analytical toolkit, making strides in derivative pricing, portfolio optimisation, and risk management.
What is Itô’s Lemma?
Itô’s Lemma is a mathematical rule used to analyse and solve stochastic differential equations (SDEs). These equations are fundamental in modelling the dynamics of financial instruments, such as stocks or options, which are influenced by deterministic factors (e.g., expected return) and random noise (e.g., market volatility). The Lemma allows us to describe how a function of a stochastic process evolves in time, which is particularly useful in financial models like the Black-Scholes formula for option pricing.
In plain terms, Itô’s Lemma helps us break down complex relationships between variables, providing a way to approximate or calculate the evolution of a financial metric—such as the logarithm of stock prices—under uncertainty.
Python
Python has emerged as a leading language for quantitative finance due to its extensive libraries and user-friendly syntax. Libraries such as NumPy and Matplotlib simplify the implementation of Itô’s Lemma, enabling quants to simulate stochastic processes, visualise results, and generate actionable insights quickly. Python’s flexibility allows seamless integration with machine learning and other advanced analytics techniques.
Modelling stock prices
Consider a stock price modelled using Geometric Brownian Motion (GBM), a widely used process in finance. GBM accounts for the deterministic drift (expected return) and the random walk (market volatility). By applying Itô’s Lemma, quants can derive key metrics such as logarithmic returns and sensitivities or even simulate price paths under different scenarios.
How Python and Itô’s Lemma can add value:
Simulating price movements
Using GBM, quants can simulate how a stock’s price evolves in time, incorporating real-world uncertainty through random noise. Python’s NumPy library allows efficient generation of these simulations, providing the foundation for scenario analysis or stress testing.
Logarithmic price approximation
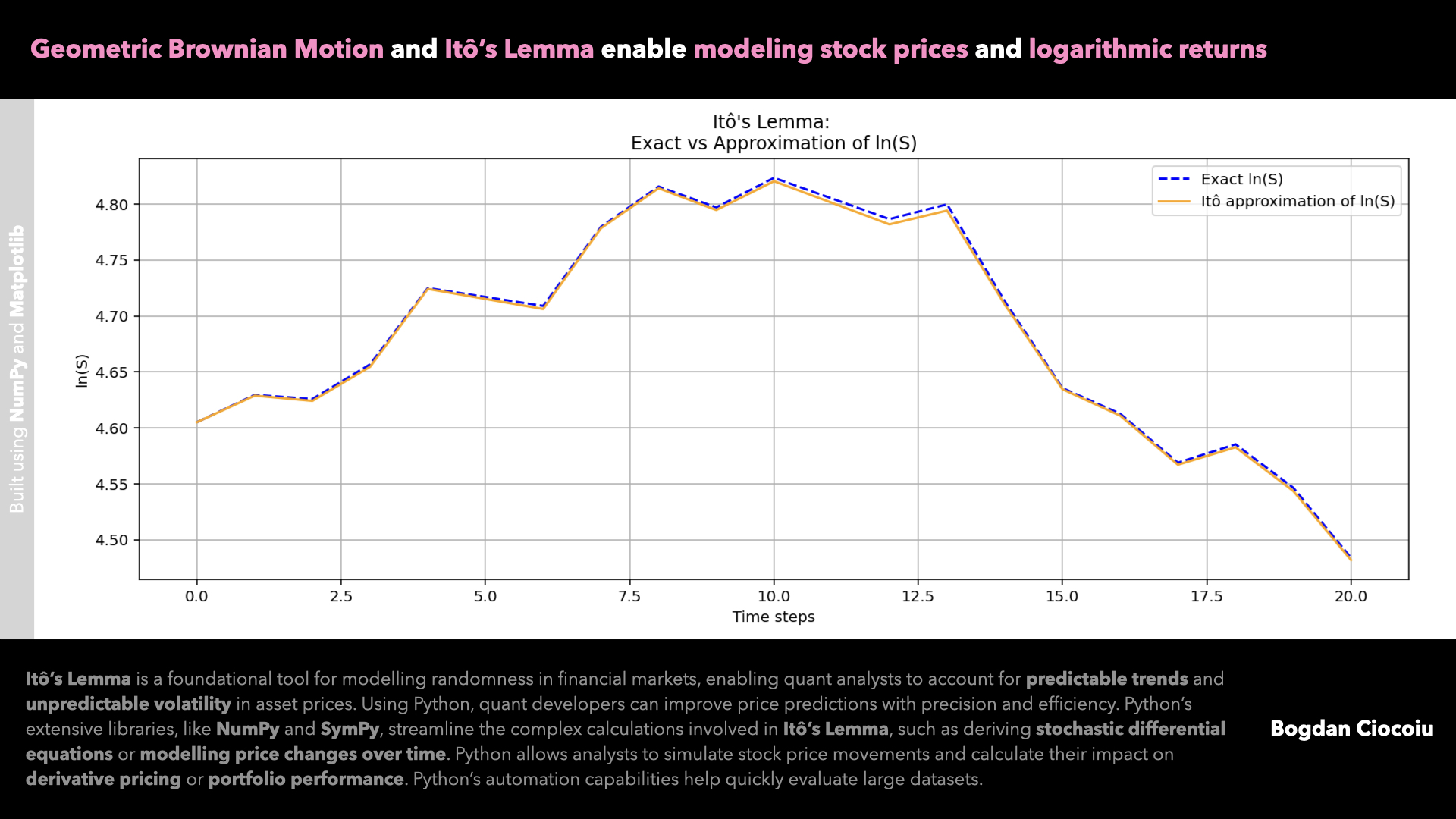
Itô’s Lemma enables the approximation of a stock’s logarithmic price, which is critical for analysing returns or constructing derivative pricing models. Python simplifies this through straightforward calculations and iterative logic.
Visualising accuracy
With Matplotlib, quants can compare exact stock price dynamics to approximations generated using Itô’s Lemma. These visualisations validate the mathematical model and provide clear insights into its accuracy across various market conditions.
Benefits for quant analysts
- Enhanced accuracy
- Scenario analysis
- Educational insights
- Seamless integration
Quantitative analysts can elevate their financial modelling capabilities by combining the mathematical rigour of Itô’s Lemma with Python’s computational power.
Leave a Reply
You must be logged in to post a comment.