Delta hedging is an essential technique in options trading, allowing traders to mitigate the risk of price fluctuations in the underlying asset. With Python, quant developers can access powerful tools for implementing and optimising this strategy, turning complex theoretical models into actionable solutions.
The challenge
Delta hedging requires calculating the delta, which, in the instance of options, measures the sensitivity of an option’s price to changes in the underlying stock price. For a portfolio to remain neutral to price movements, one must adjust the hedge dynamically as market conditions change. Such scripts involve intricate calculations, which, if done manually, can be time-consuming and error-prone.
Python
Python scripts leverage the Black-Scholes model to calculate the delta and provide a structured approach to hedge adjustments. By defining parameters such as the stock price, strike price, time to maturity, risk-free interest rate, and volatility, Python scripts set up a foundation for accurate computations.
Python uses the Black-Scholes formula to compute the delta for a given stock price. Initially, the algorithm determines the number of shares to hold to hedge a 10-option position. It then simulates a change in the stock price and recalculates the delta for the new conditions, determining the necessary adjustment to the hedge.
Python’s extensive libraries, such as NumPy for numerical calculations and Matplotlib for visualisation, make it an ideal choice for financial modelling.
Visualisation
Python’s most significant advantage is its ability to transform data into insights through visualisation. Python scripts employ Matplotlib to generate two key visualisations:
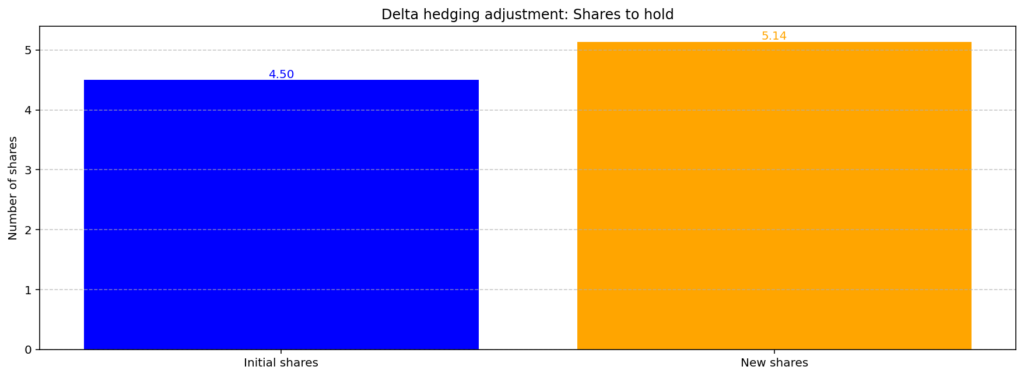
A bar chart comparing the initial hedge position with the adjusted position after a stock price change offers an intuitive view of the required adjustments.
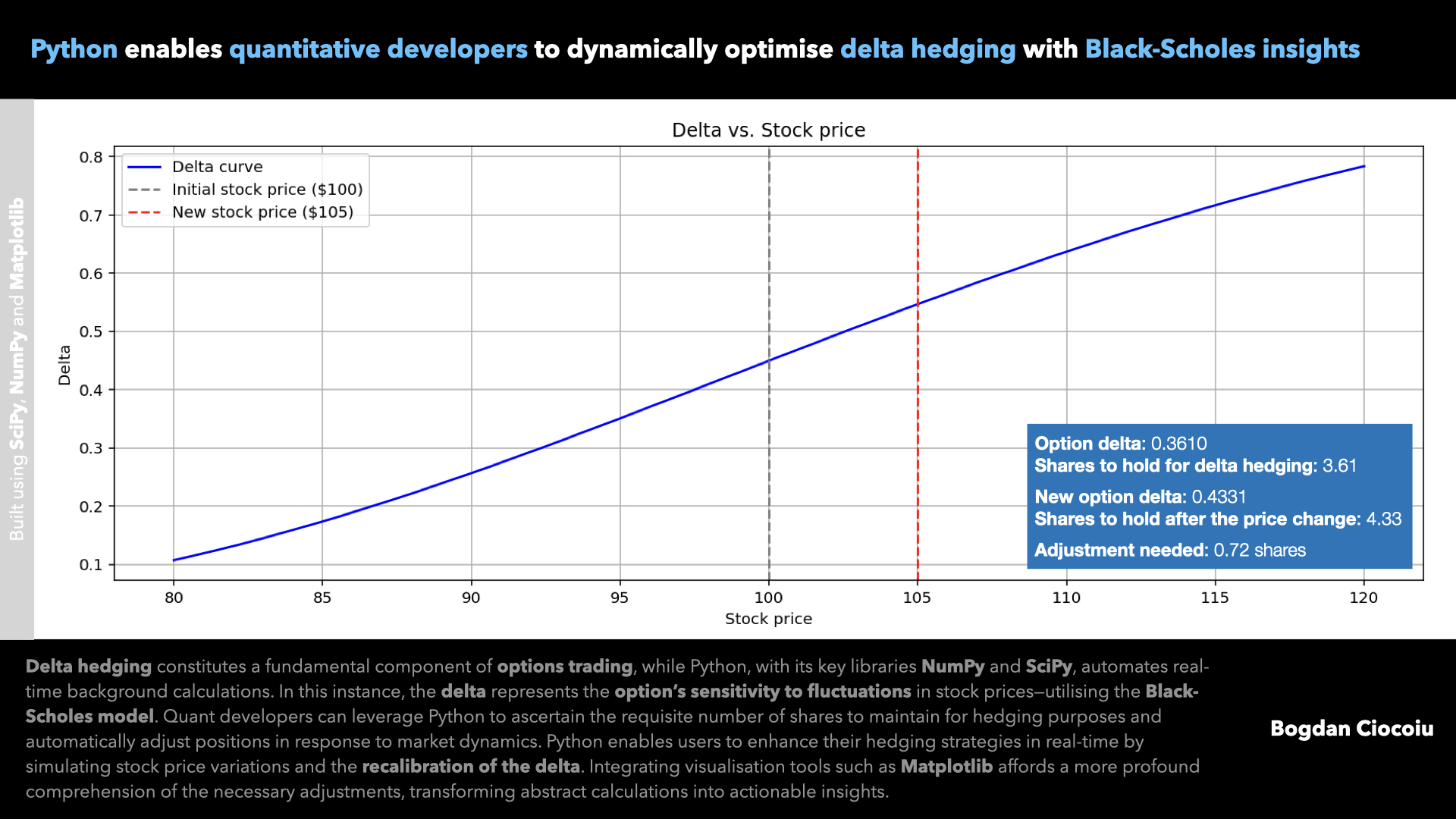
A delta curve illustrating how delta evolves across a range of stock prices helps traders understand the sensitivity of their option positions to market movements.
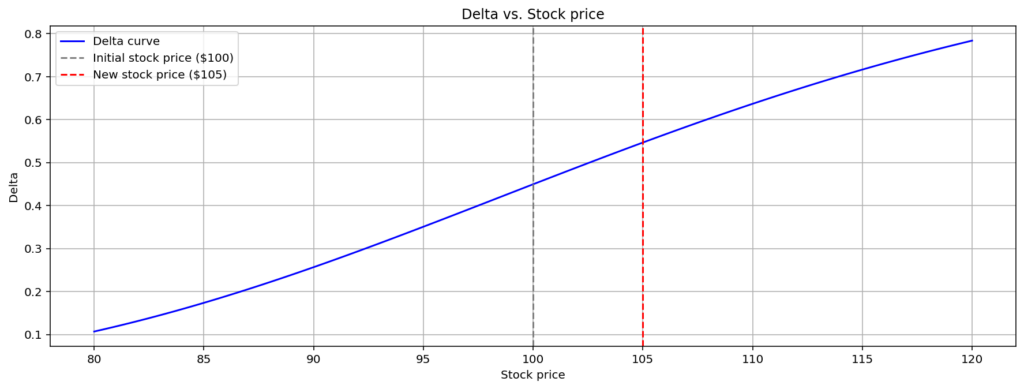
These visualisations bridge the gap between abstract calculations and practical decision-making, making communicating complex strategies to stakeholders easier.
Analysis output
Option delta: 0.3610
Shares to hold for delta hedging: 3.61
New option delta: 0.4331
Shares to hold after the price change: 4.33
Adjustment needed: 0.72 sharesPractical benefits for quants
- Python automates the repetitive calculations involved in delta hedging, saving developers significant time.
- Real-time recalculations ensure that portfolios remain balanced, even in volatile markets, reducing exposure to unforeseen losses.
- Such scripts support extensive portfolios, making Python versatile for various use cases.
- The visualisations enable traders to understand when and how to adjust hedging strategies.
Python’s role in delta hedging is a testament to its versatility and power in quantitative finance. Python enables quantitative developers to address real-world challenges with precision and efficiency, from automating complex calculations to visualising actionable insights.
Leave a Reply
You must be logged in to post a comment.