Martingale properties

Martingale properties lie at the core of modern financial theory and quantitative analysis. These properties describe stochastic processes where the conditional expected value of the next observation, given the current and past values, equals the current observation. 

In simple terms, martingales represent “fair games” where no arbitrage opportunities exist. This principle is pivotal inrisk-neutral pricing and forms the theoretical backbone of derivative valuation models.

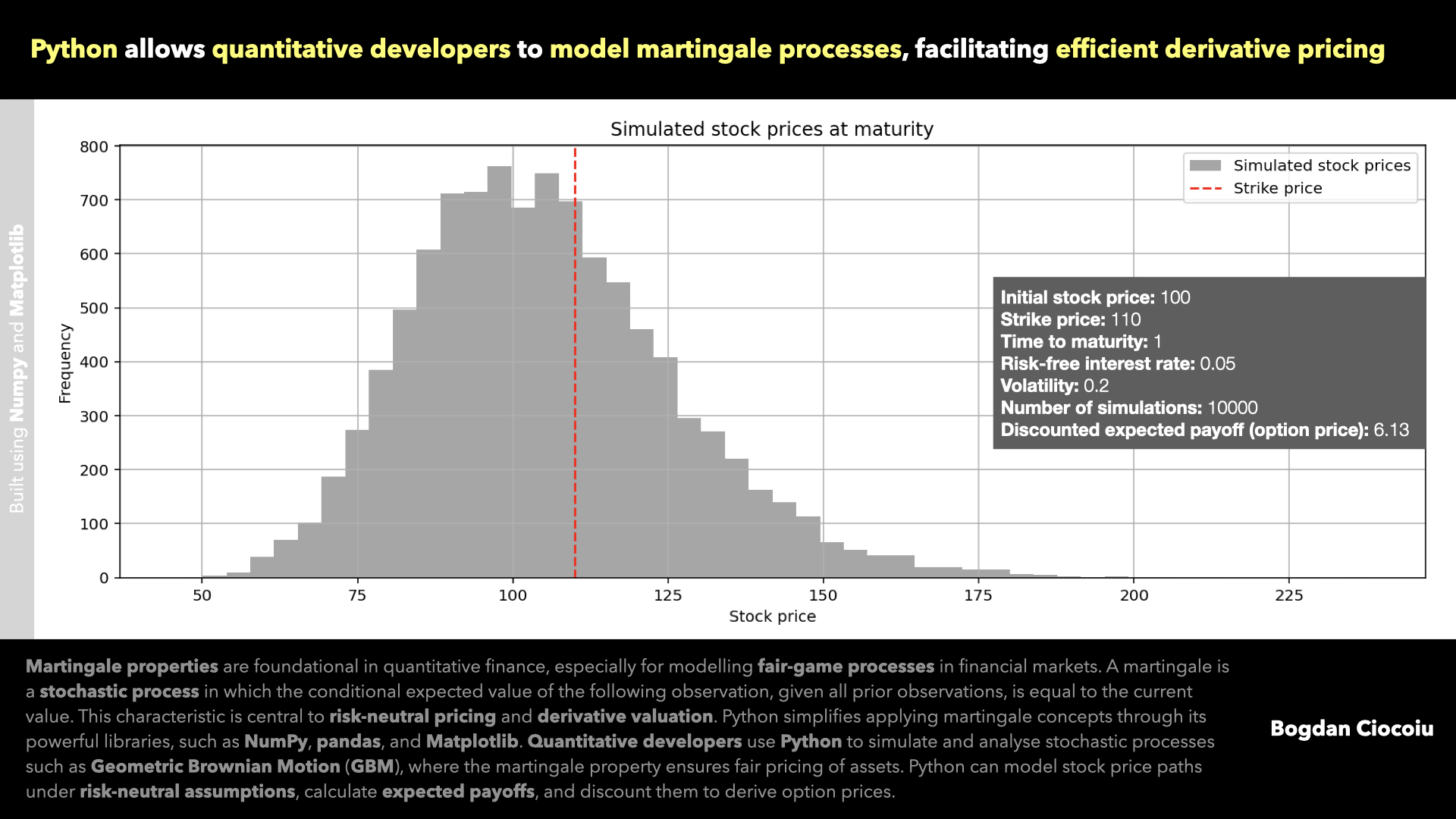
In a martingale process, the future value of a stock, adjusted for the risk-free rate, is expected to equal its current value, which ensures that financial markets operate under efficient and arbitrage-free conditions. 

With its extensive library ecosystem, Python provides an ideal platform for implementing and analysing martingale properties in financial models.

Why Python?

Python’s flexibility and computational capabilities make it a go-to language for financial modelling, especially for tasks involving stochastic processes and martingale properties. Libraries like NumPy, pandas, and Matplotlib enable quantitative developers to simulate, analyse, and visualise financial data efficiently.

1. Python can simulate stochastic processes like Geometric Brownian Motion (GBM) and Wiener processes. These are widely used in modelling asset prices, which are assumed to follow a martingale process under risk-neutral measures. Using NumPy, developers can generate random noise, model price paths, and validate whether the martingale property holds.
2. In derivative pricing, the martingale property ensures that the discounted payoff’s expected value equals the derivative’s current price. Python facilitates these calculations by automating simulations and applying discounting factors to derive fair prices.
3. Python’s visualisation libraries, such as Matplotlib and Seaborn, provide developers with tools to validate martingale properties visually. Developers can assess whether the process satisfies the martingale condition by plotting simulated asset price paths and corresponding discounted values.

Python easily handles large-scale simulations and analyses, making it ideal for real-world financial applications. Python integrates seamlessly with databases, APIs, and other financial tools, streamlining data retrieval and processing.

Python’s libraries transform abstract mathematical properties into intuitive visuals, aiding decision-making and stakeholder communication. Being open-source, Python eliminates the need for expensive proprietary software, making it accessible to firms of all sizes.

Applications in financial markets

Martingale properties have diverse applications in finance, and Python makes these applications practical and scalable:

• Option pricing
• Hedging strategies
• Algorithmic trading
• Portfolio optimisation

Python empowers quantitative developers to explore and apply martingale properties effectively in financial modelling. From simulating stochastic processes to implementing risk-neutral pricing, Python’s robust ecosystem transforms theoretical concepts into practical solutions.